分類問題
スパムメールを判別するような問題は一般的に「分類問題」として機械学習では取り扱う。分類問題とはいまある「物」や「発生した事柄」を確率的に分類する。この「確率的」という言葉がみそであり、固定されたルールに従っているわけではなく、機械学習により構築されたモデルにより判別される。
条件付き確率およびベイズ定理
分類問題の判別に用いられるアルゴリズムで最も基本的となるのがベイズ定理である。このベイズ定理を理解するためには「条件付確率」を理解しておく必要がある。
条件付確率
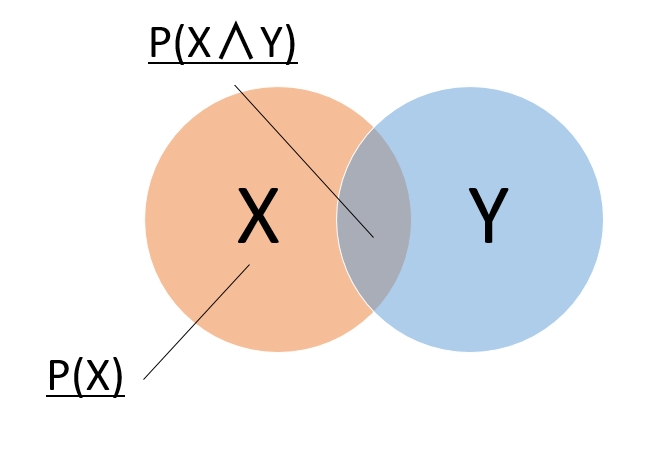
条件付き確率とはある事象Xが発生したという前提で事象Yが発生する確率である。条件付確率は以下のようにあらわされる。
$$P( Y | X )=\frac{P(X∧Y)}{P(X)}$$
ベン図にすると以下のようになる。
ベイズ定理
ベイズ定理は以下のようにあらわすことができる。
$${P(X|Y)}\times{P(Y)}={P(Y|X)}\times{P(X)}$$
ベイズ定理の証明は統計サイトなどに詳しく記載されているのでそちらを参照。上記式を変形すると以下のようになる。
$$P(X|Y)=\frac{P(Y|X)\times{P(X)}}{P(Y)}$$
さてポイントとなるのはこのベイズ定理がどのように分類問題で利用されるかである。
ベイズ定理と分類問題
スパムメール判別問題を例にしてベイズ定理をどのように分類問題に利用するかを説明する。
スパムメールの判別問題はある一通のメールからそのメールに含まれている単語をもとにしてスパムメール(spam)か普通メール(ham)を判断する。
今下記のように確率を定義する。
$$P(spam) = スパムメールである確率$$
$$P(ham) = 普通のメールである確率$$
$$P(mail) = ある単語が出現する確率$$
今条件付き確率を考えると以下のようになる。
$$P(mail | spam) = スパムメールに対してある単語が現れる確率$$
$$P(mail | ham) = 普通のメールに対してある単語が現れる確率$$
最終的に知りたいのは以下である。
$$P(spam|mail) = ある単語が出現したときに、スパムメールである確率$$
$$P(ham|mail) = ある単語が出現したときに、普通メールである確率$$
あるメールがスパムメールであると判断するときにはいくつか方法がある。例えばある単語が出現したときに、スパムメールである確率>普通メールであると確率なら、スパムと判断する方法がある。
$$P(spam|mail) > P(ham|mail)$$
ではどのようにして P(spam|mail)とP(ham|mail)を計算するのか。ここで利用するのがベイズ定理である。いまベイズ定理を利用すると以下のようになる。
$$ P(spam|mail) = \frac{(P(mail|spam)\times{P(spam)}}{P(mail)}$$
$$ P(ham|mail) = \frac{(P(mail|ham)\times{P(ham)}}{P(mail)}$$
ここでP(mail | spam)についてはスパムメールとしてラベルがついているメールに対して単語の出現頻度を計算すれば取得できる。P(spam)はすべてのメールに対するスパムメールの割合を計算すればよい。P(mail)は全メールに対して単語の出現頻度を計算すればよい。
P(mail|ham)は同様にして普通メールに対して単語の出現頻度を計算する。またP(ham)は普通のメールが全体に占める割合である。
このようにしてP(spam|mail)およびP(ham|mail)をベイズ定理により計算して、分類をする学習器がナイーブベイズである。
ナイーブベイズ分類樹
ナイーブベイズがもっともよくつかわれるが、単語による文書分類である。簡単な例を通してナイーブベイズによる文書分類を説明する。
今下記のような各国について説明した文章があるとする(このデータは全く恣意的なデータである)。
| 国 | データ |
| アメリカ | 海、都市、遊園地 |
| タイ | 海、遺跡、都市、食事 |
| 中国 | 遊園地、歴史、夜景、買い物 |
| フランス | 海、食事、都市 |
| アメリカ | 都市、食事 |
今下記の分類データが渡されたときのカテゴリを計算する。
[海、都市]
事前確率(各カテゴリが出現する確率)
いま各カテゴリが出現する確率を考える。これは以下のように計算される。
$$P(category )=\\frac{各カテゴリの文書数}{全部の文書数}$$
| カテゴリの文書数 | 全文書数 | P(Category) | |
| アメリカ | 2 | 5 | 2/5 |
| タイ | 1 | 5 | 1/5 |
| 中国 | 1 | 5 | 1/5 |
| フランス | 1 | 5 | 1/5 |
尤度(各カテゴリにおける分類データが出現する同時確率
各カテゴリにおいて分類データが出現する同時確率を求める。
$$ P(word | category) = \frac{P(word∧category)}{P(category}$$
| カテゴリ内総単語数 | 海 | 都市 | 同時確率 | |
| アメリカ | 5 | 1 | 2 | 2/25 = 1/5 x 2/5 |
| タイ | 4 | 1 | 1 | 1/16 = 1/4 x 1/4 |
| 中国 | 4 | 0 | 0 | 0 |
| フランス | 3 | 1 | 1 | 1/9 = 1/3 x 1/3 |
事後確率 (分類データが与えられた時のカテゴリが出現する確率)
| 事前確率 | 尤度 | 事後確率 | |
| アメリカ | 2/5 | 2/25 | 4/125=0.032 |
| タイ | 1/5 | 1/16 | 1/80=0.0125 |
| 中国 | 1/5 | 0 | 0 |
| フランス | 1/5 | 1/9 | 1/27=0.037 |
よって[海、都市]というデータが与えらた時にはナイーブベイズではフランスと分類される。