データの説明

1949～1960年における月別飛行機搭乗者数

フォーマット

このデータは時系列データであることがわかる。

> str(AirPassengers)
 Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121

時系列データは定期的な時間に従って記録されたデータである。Rでは時系列データのための関数が用意されている。時系列データである場合にはまず以下の確認をする。

• 時系列のパラメータを確認する
• 全体的なトレンドを確認する
• 周期的なトレンドを確認する

時系列パラメータの確認

確認をする前にデータセットの名前を短くして、扱いやすくする。

> AP = AirPassengers

データの開始と終了を時間を確認すると、開始は1949年の1月からであり、1960年12月までのデータが得られていることがわかる。

> start(AP)
 [1] 1949    1
 > end(AP)
 [1] 1960   12

次に観察の頻度を確認する。観察は1サイクル12、よって月ごとに行われている。

> frequency(AP)
 [1] 12

具体的な時間の頻度を知りたい場合にはtime()を使う。

> time(AP)
 Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
 1949 1949.000 1949.083 1949.167 1949.250 1949.333 1949.417 1949.500 1949.583
 1950 1950.000 1950.083 1950.167 1950.250 1950.333 1950.417 1950.500 1950.583
 1951 1951.000 1951.083 1951.167 1951.250

cycle()により周期がわかる。

> cycle(AP)
     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949   1   2   3   4   5   6   7   8   9  10  11  12
1950   1   2   3   4   5   6   7   8   9  10  11  12
1951   1   2   3   4   5   6   7   8   9  10  11  12
1952   1   2   3   4   5   6   7   8   9  10  11  12

全体的なトレンドを確認する

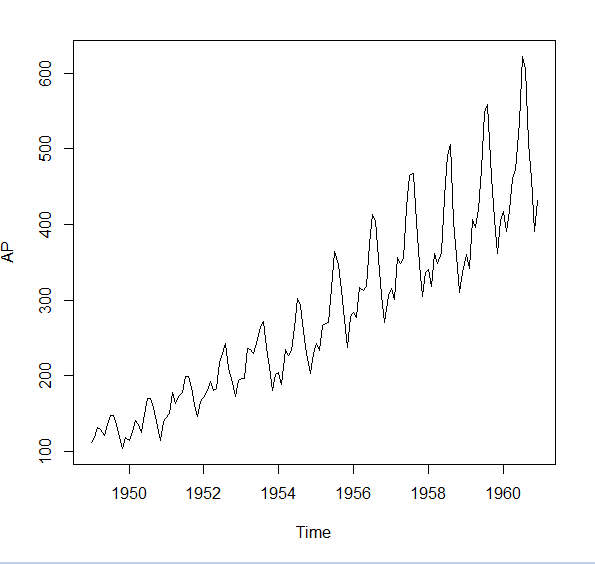
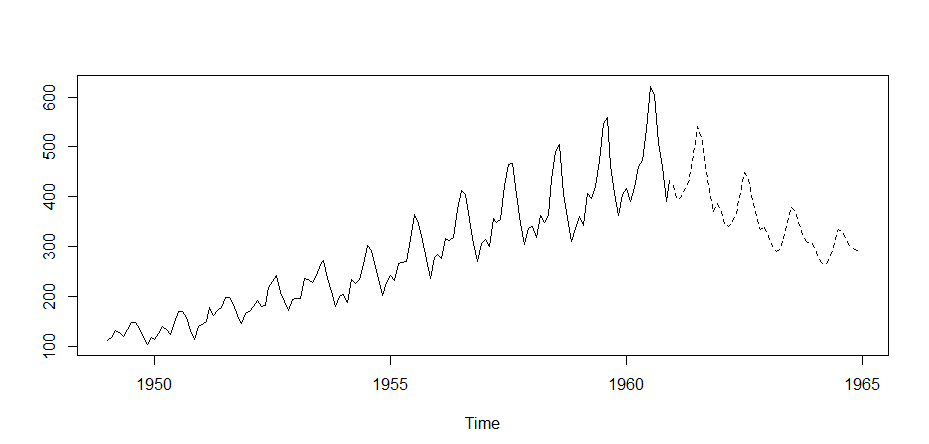
> plot(AP)

トレンドを確認すると長期的に増加傾向にあると同時に1年の中でも変動がある。それ以外には短期的な要因による変化（ストイスキャティック）があるのでこれらの要因をバラバラにして確認する。

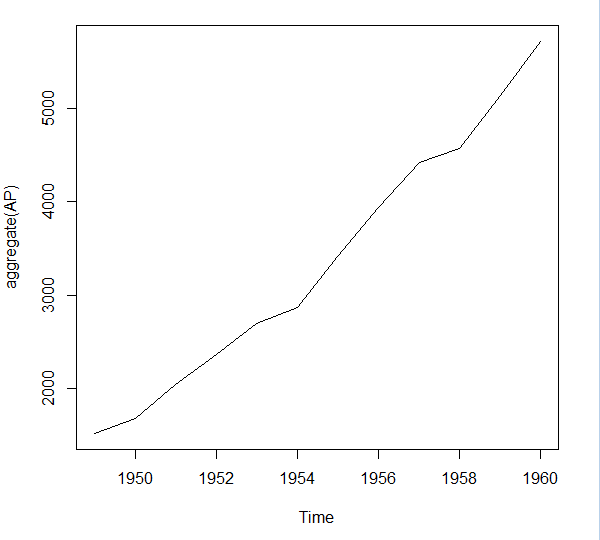
年で合計してトレンドを見てみる

> aggregate(AP)
Time Series:
Start = 1949 
End = 1960 
Frequency = 1 
 [1] 1520 1676 2042 2364 2700 2867 3408 3939 4421 4572 5140 5714

plot(aggregate(AP))

季節要因を取り除くと長期的にも増加傾向にあることがわかる。よって搭乗員数の増加にはビジネスにおける飛行機利用の増加、人口の増加、航空券価格の低下などが関連していると考えられる。

•  ビジネス客のトレント
• 人口トレント
• 航空券価格との関連

季節ごとの変動を調べる

次に季節ごとにおける搭乗者数の変化を見てみる。

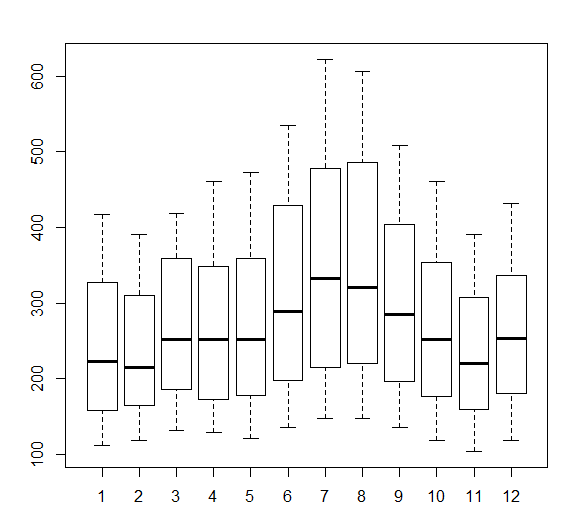
 boxplot(AP ~ cycle(AP))

季節ごとの変動から以下のことが読み取れる

• 平均は7月および8月がツートップ。
• 1月から7月にかけて上昇し、7月で最大となったのち、11月まで下降する。12月には一時的に増加するが、1月で減る。
• 年を通すと、1月, 2月, 11月が少ない。
• 季節ごとの散らばり具合は7月と8月で大きい。
• ３～5月は平均はほぼ同じだが、4，5月になるとその年により変動が大きくなる。

考察してみる

• 7月および8月は夏休みで搭乗者数が多くなると考えられる。年ごとに観光のトレンドが変わるために変動幅が大きいと考えられる。
• 夏休みは6月～9月にとられるが、後半より前半にとる人が多い。
• クリスマスは思ったより人の移動は少ない。
• 人の移動は３～5月でほぼ同じだが、４，５月は気候により人の移動が変わると考えらえる。

自己相関分析

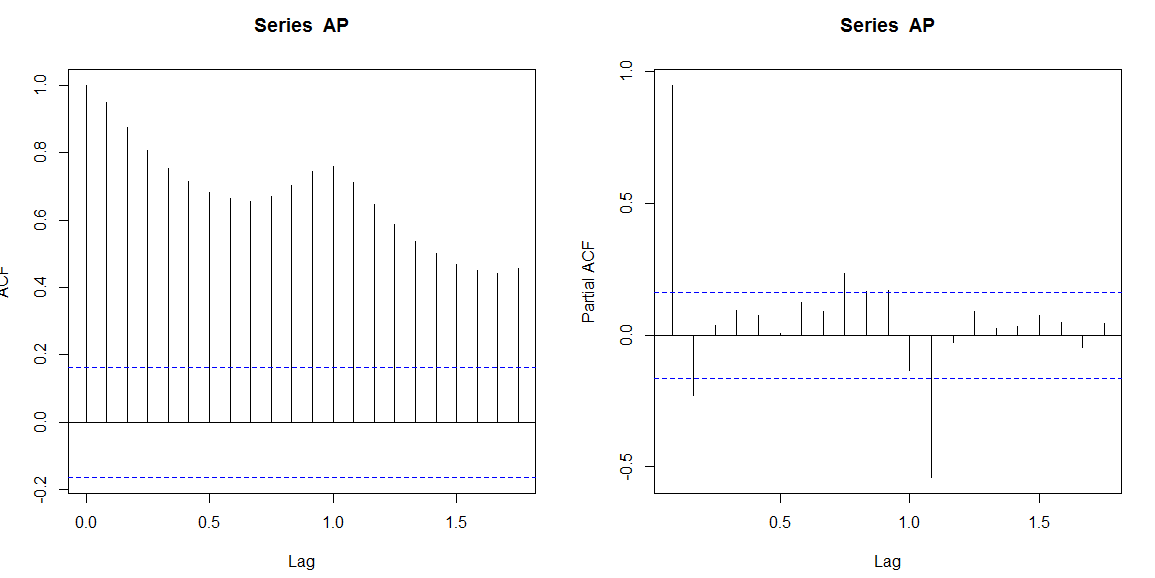
過去データから予測が可能であるか自己相関分析をしてみる。

> par(mfrow=c(1:2))
> acf(AP)
> pacf(AP)

単位根検定

自己相関モデルを作るために単位根検定を実施し定常であるかを確認する。単位根検定の帰無仮説は”非定常である”であり、棄却されれば単位根がないために定常であると結論付ける。

単位根である場合には本来相関がないにもかかわらず相関係数が高く出やすく、見せかけの相関になる可能性がある。

ただし単位根であっても長期的に相関がある場合には相関モデルを作ることはできるので単位根検定のみの結果に依存することはない。

> PP.test(AP)
        Phillips-Perron Unit Root Test
data:  AP 
Dickey-Fuller = -5.0489, Truncation lag parameter = 4, p-value =
0.01
> adf.test(AP)
        Augmented Dickey-Fuller Test
data:  AP 
Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01
alternative hypothesis: stationary 

 警告メッセージ： 
In adf.test(AP) : p-value smaller than printed p-value

自己回帰モデル

RでAirline Passengerの自己回帰モデルを構築する。

自己回帰モデルはar()で作成する

> AP.ar <- ar(AP)

summary()で結果を確認する。

> summary(AP.ar)
             Length Class  Mode     
order          1    -none- numeric  
ar            13    -none- numeric  
var.pred       1    -none- numeric  
x.mean         1    -none- numeric  
aic           22    -none- numeric  
n.used         1    -none- numeric  
order.max      1    -none- numeric  
partialacf    21    -none- numeric  
resid        144    ts     numeric  
method         1    -none- character
series         1    -none- character
frequency      1    -none- numeric  
call           2    -none- call     
asy.var.coef 169    -none- numeric

上記より自己回帰モデルの次数は13であることがわかる。13というのは微妙な数字で前年同月が含まれる。当然前年同月とは季節変動による影響が同じであるから、相関が高くなることが予測される。しかし回帰モデルとしては、例えば前6か月分くらいのデータから予測できるほうが全体的なトレンドのみを含むことができるので、時間経過にあった予測となる。

係数を確認してみる。

> AP.ar

Call:
ar(x = AP)

Coefficients:
      1        2        3        4        5        6        7        8  
 1.0131  -0.0544  -0.0418   0.0188   0.0387  -0.0780   0.0248  -0.0710  
      9       10       11       12       13  
 0.0655  -0.0586   0.1941   0.4508  -0.5397  

Order selected 13  sigma^2 estimated as  906.1

やはり前年同月が係数として最も高く0.4508、次いで前年次月の0.1941となる。これは季節変動が大きいことを意味する。前年前月の係数が-0.5397と負の相関がつよい理由がよくわからない。

リュング・ボックス検定

リュング・ボックス検定により残差が独立であるかを確認する。リュンブ・ボックス検定での帰無仮説は集団は無作為（独立）であるとなる。棄却されれば、集団は無作為ではないために自己回帰モデルを使用することができない。

Rではリュング・ボックス検定はBox.test()で実施する。

> Box.test(AP.ar$res)

        Box-Pierce test

data:  AP.ar$res 
X-squared = 0.5698, df = 1, p-value = 0.4503

結果は0.45となるので、どちらともいえる。

予測

自己回帰モデルを使って次の一年についてAirline Passengerを予測してみる。

> AP.predict <- predict(AP.ar, n.ahead=12)
> AP.predict
$pred
          Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
1961 422.9124 394.1377 399.9245 416.1096 434.5472 483.3833 541.7503 521.9440
          Sep      Oct      Nov      Dec
1961 459.3654 412.0265 369.9949 387.5387

$se
          Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
1961 30.10181 42.85080 51.88776 58.36698 63.40902 67.85779 71.15245 73.73242
          Sep      Oct      Nov      Dec
1961 75.29300 76.46974 77.13687 78.20550

予測データをプロットしてみる。

 ts.plot(AP, AP.predict$pred, lty=1:2)