エクセルでの単回帰分析をについて手順をまとめる。エクセルの使い方にあわせて分析結果の解釈の仕方も書いておく。
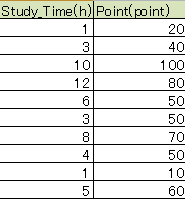
データは勉強時間に対する点数とする。これは作ったデータであるが、線形回帰にフィットするようにしてある。
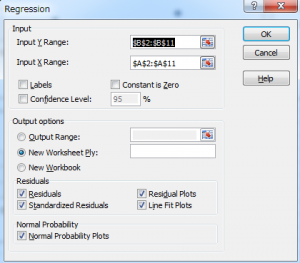
Excelの回帰分析を立ち上げる。予測変数と応答変数以外に設定するポイントとしてはresidualがある。回帰分析の結果だけをほしいのであればresidualは必要ない。単回帰分析であれば相関係数、係数、切片が得られれば報告書は作成できる。しかし得られた結果が信頼できるかを確認するためにはいくつかの検証をする必要がある。resisualのデータによりモデルが適切であるかを判断できる。
回帰分析を実行すると以下のような結果が得られる。
- R Squareが高いことを確認する。R Squareは応答変数の変化に対する予測変数の割合を示す。ここではポイントの変化のうち82.68%が勉強時間によって説明されている。複数のモデルで比較する場合には、R Squareが最も高いモデルを利用する。このモデルは単位回帰であるので比較はできないが、82.68%を説明できるのは高いといえる。
- F検定で帰無仮説: すべての予測子=0であるかを検定する。ここではp=0.000265となっているのでいづれかの予測子は応答変数に効果があることがわかる。今回は予測子は勉強時間である。よって勉強時間の係数は0ではないことがわかる。
- X Variablのt検定の結果を見ると p=0.000265である。よって勉強時間はPointに対して有意な予測子であることがわかる。
- 係数は 6.5である。よって勉強時間を1時間増やすとポイントが6.5上がる。
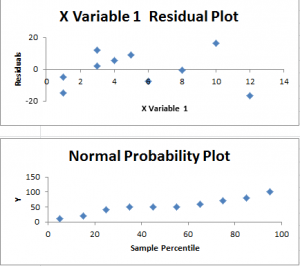
次に残渣について確認する。
モデルが適切であるならば、残差は規則性はなくランダムである。この時残差は平均値0であり、一定の標準偏差をもつ正規分布からに従う。残差のプロットを確認してみると規則性はない(線形、横V字、U字など)。またPPプロットはほぼ直線であるので正規分布に従っていると推定される。
結論
ポイントについて62.83%の変化は勉強時間で説明できることがわかった。勉強時間の係数hあ6.5であり、これは勉強時間を1時間増やすとポイントが6.5増えることを意味する。また残差はランダムであり正規分布に従っているために、ポイントに対する予測子は勉強時間のみで十分といえる。