リッジ回帰はL2ノルムの正則項を導入することで、過学習を防ぐ。この場合過学習を防ぐとは、重みを0の方向に動かすという意味である。実際に線形回帰とリッジ回帰を比べてみて、どのようにモデルが変わるかを確認する。
線形回帰
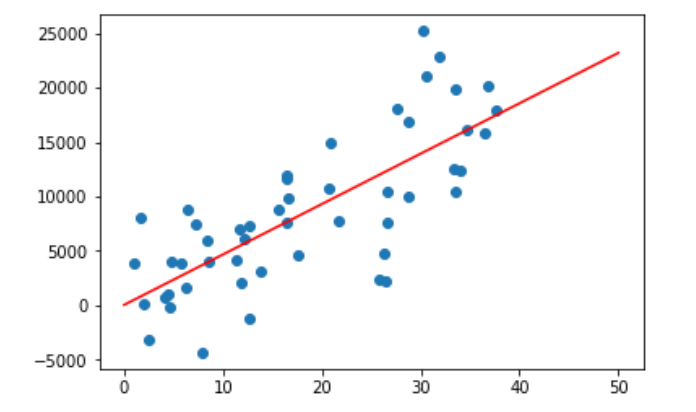
アイスクリームの売り上げを考えて、1~37度に対してランダムの売り上げデータを生成する。
import matplotlib.pyplot as plt import seaborn as sns; import numpy as np %matplotlib inline import random rng = np.random.RandomState(1) x = 37 * rng.rand(50) + 1 # 1度から3度 y = 500 * x - 5000 * rng.randn(50) # 売り上げデータはおよそ気温の500倍想定、ただしノイズを組みこむ
次に線形回帰を行う。
# 線形回帰 from sklearn.linear_model import LinearRegression model_lr = LinearRegression(fit_intercept=True) model_lr.fit(x[:, np.newaxis], y) xfit = np.linspace(0, 50, 1000) yfit_lr = model.predict(xfit[:, np.newaxis]) plt.scatter(x, y) plt.plot(xfit, yfit_lr,color="red", label="LinearRegression");
リッジ回帰
リッジ回帰はRidgeを用いる。
sklearn.linear_model.Ridge — scikit-learn 0.21.3 documentation
Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver=’auto’, random_state=None)
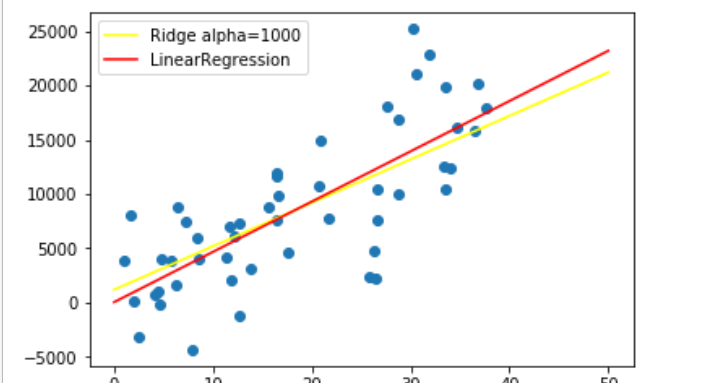
もっとも重要なのがalphaである。alphaは正則項の強さを指定する。
# リッジ回帰 from sklearn.linear_model import Ridge model_r = Ridge(alpha=1000) model_r.fit(x[:, np.newaxis], y) yfit_r = model_r.predict(xfit[:, np.newaxis]) plt.scatter(x, y) plt.plot(xfit, yfit_lr,color="red", label="LinearRegression"); plt.plot(xfit, yfit_r, color="yellow", label="Ridge alpha=1000") plt.legend()
リッジ回帰のモデルは重みづけが小さくなっていることがわかる。