線形回帰
世の中の様々な出来事(y)はある事象(x)に対して比例することが多い。もちろん厳密に比例するわけではなくずれは生じる。しかしこのxとyが比例すると仮定した場合、中学校で習った一次式でこの関係をとらえることができる。
$$ y = a \times x + b $$
この時xを説明変数、yを目的変数という。線形回帰では説明変数をもとにして目的変数を計算する一次式を明らかにする。これを線形回帰と呼ぶ。
線形回帰の際には(x, y)の組み合わせのデータが用意される。このデータを基にしてaおよびbを算出することができる。
実データと線形回帰
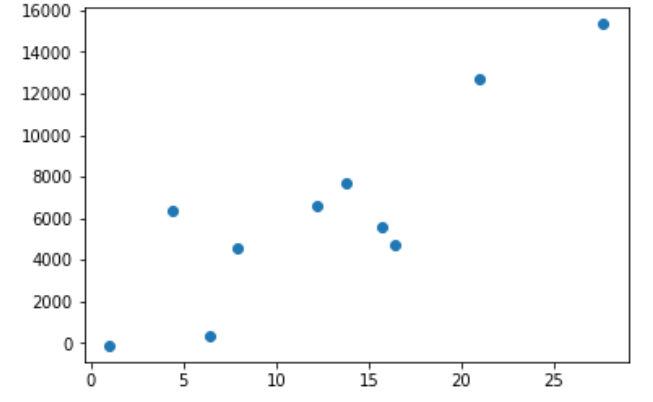
いま気温とアイスクリームの売り上げを考える。10日の気温と売り上げを記録したところ以下のようになったとする。
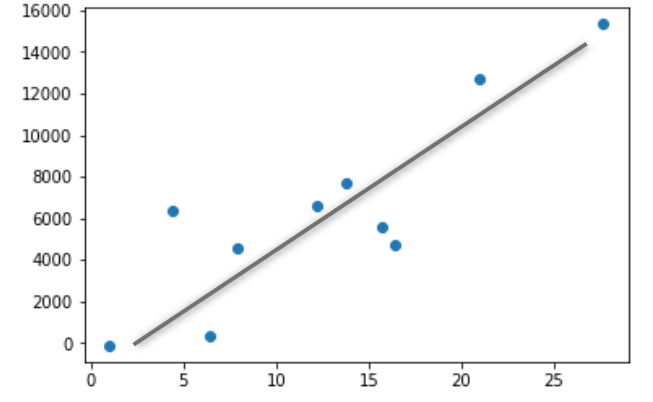
ずれはあるものの気温と売り上げデータには比例関係があり以下のように直線が引ける。
これを一次式であらわすと以下のようになる。
$$ アイスクリームの売り上げ = Θ_1\times 気温 + Θ_0 $$
この時アイスクリームの売り上げが目的変数となり、気温が説明変数となる。
Θ1は気温に対する重みである。重みとは気温がどの程度アイスクリームの売り上げに影響を及ぼすかの指標である。Θ1が小さければ、気温は売り上げに影響しない。それに対してΘ1が大きくなるほど売り上げは気温により左右されることになる。
このΘ1およびΘ0を明らかにできれば、アイスクリームの売り上げと気温の関係を導き出すことができる。これを線形回帰と呼ぶ。
最小二乗法
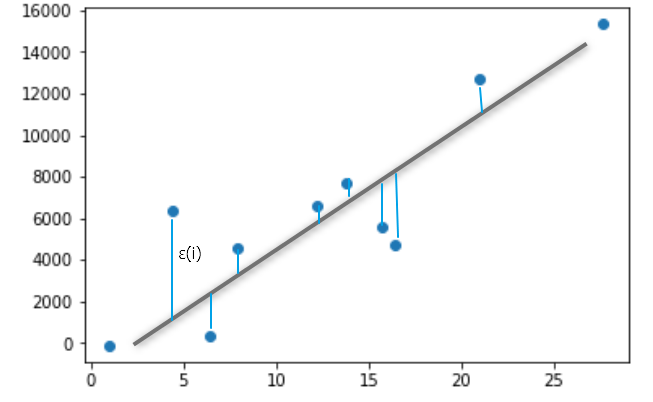
ではどのようにしてΘ1およびΘ0を明らかにできるのか。この手法を最小二乗法と呼ぶ。得られたデータを見るとどのような直線を描いたとしてずれが生じる。
この時ずれをε(i) = ε(1),ε(2),ε(3),,,,,ε(n)とする。 これはデータの組み合わせ(x(i), y(i))に対してそれぞれのデータについて引いた直線のずれを表す。
このずれは直線の式を用いると以下のようにあらわすことができる。
$$ ε_i = y_i – Θ_1 \times x_i – Θ_0 $$
データに対してフィットした直線とはこのずれの合計が最も小さくなる直線を探す。ずれの合計は以下のようにあらわすことができる。
$$ E_Θ = \sum_{i=1}^{n}( ε_i )^2$$
よって一次式であらわすと以下のようになる。
$$ E_Θ = \sum_{i=1}^{n} (y_i – Θ_1 \times x_i – Θ_0)^2 $$
この式を2乗誤差の損失関数と呼ぶ。この関数は他の損失関数と比べて外れ値に大きく左右される。
最急降下法
さて最小二乗法を利用すれば、Θ0およびΘ1を求めることができるようである。またそのカギは以下の式である。しかしどのようにしてΘ0およびΘ1を求めればよいのか。ここで利用するのが最急降下法という技である。
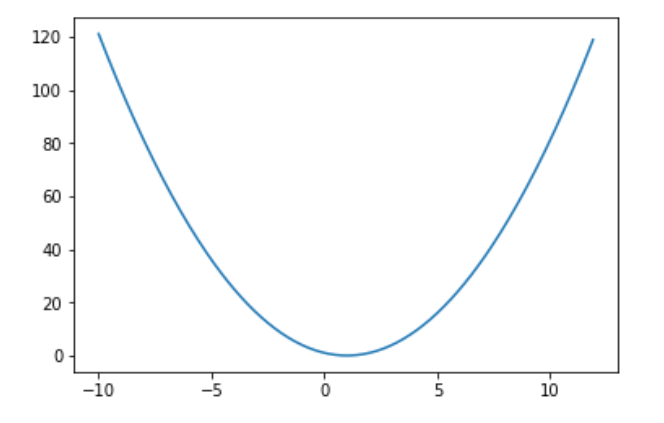
いま下記のようなグラフを考える。
これは以下の方程式をグラフにしたものである。
$$ y = (x-1)^2 $$
このグラフの最小値を求めたいとき、どのようにすればよいか。最小値があらかじめわかっていれば、yに最小値を代入して、方程式を解くことができる。しかしそもそも最小値がわからないために代入できない(今回の場合には例が単純であるが)。では最小値の左と右で値の増減がグラフから見てみる。
| yの増減 | |
| 最小値の左側 | 減っている↓ |
| 最小値 | 0 |
| 最小値の右側 | 増えている↑ |
上記のことがわかっている。ここでyの増減を数式であらわすためには微分を用いることになる。微分を用いると以下のようにあらわされる。
| yの増減 | 微分 ( $$ \frac{dy}{dx} $$ ) | |
| 最小値の左側 | 減っている↓ | - |
| 最小値 | 0 | 0 |
| 最小値の右側 | 増えている↑ | + |
いまあるx=-3から最小値を探すとする。この時傾きは-であるから、次は新しいxは今のxよりも大きい値、つまり+の方向に進むことになる。いま進みすぎて傾きが+になったとする。この場合には次のxは今のxよりも小さい値となる。これを図解すると以下のようになる。
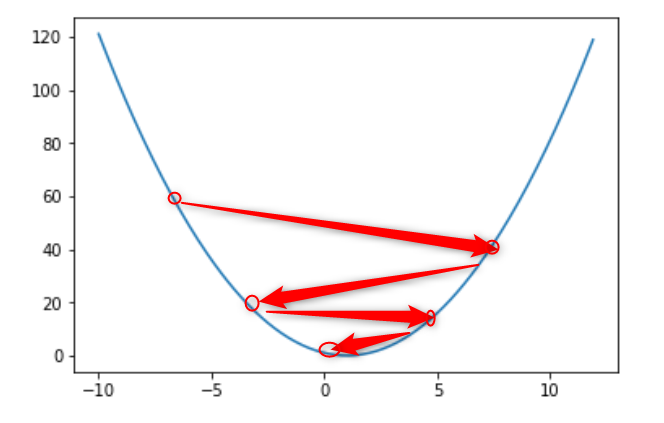
これを式に表すと以下のようになる
$$ x := x – η \times \frac{d}{dx} \times y $$
これを先ほどの損失関数に当てはめることで最急降下法により最小値を求めるのが線形回帰である。