同時確率
同時確率 = 事象XとYを考えたときにこれらが同時に起きる確率を計算する。この時同時確率は
P(X, Y) = P(X) x P(Y)
となる。
例えば2つの大きさが違うサイコロを振るとする。この時X=1になる確率は
P(X=1) = 1/6
であり、Y=1になる確率は
P(Y=1)=1/6
となる。同時確率はX=1かつY=1になる確率である。これは
P(X=1, Y=1) = P(X=1) x P(Y=1) = 1/6 x 1/6 = 1/36
となる。
条件付確率
条件付確率はXを固定したときにYが起きる確率、あるいはYを固定したときにXが起きる確率である。この確率は以下のようにあらわされる。
P(Y|X) = P(X∧Y) / P(X)
P(X=4)の時に全体の合計が10以上になる条件付確率を考える。この事象をYとする。合計が10以上になる事象は(4,6), (6,4), (5,5), (5,6), (6,5) である。よって以下のようなる。
P(X) = 1/6
P(Y) = 5/36
P(X∧Y) = 1/36
P(Y|X) = (1/36) / (1/6) = 1/6
つまりX=4が出ているときには1/6の確率で10以上になる。これは4が出た場合にはもう一つが6でないと10以上にならないので明白である。
では逆に合計10以上であるときにX=4である確率はどうなるのか。条件付確率の公式から以下が成り立つ。
P(X|Y) x P(Y) = P(Y|X) x P(X)
P(X|Y) = P(Y|X) x P(X) / P(Y)
よって
P(X|Y) = ( 1/6 x 1/6) / (5/36)
= 1/5
10になる事象は5通りであり、かつそのうちの1通りがX=4で成り立つので1/5であることが明白である。
事前確率および事後確率
いま因果関係としてAという事象が起きてからBが発生すると考える。例えばAは気温が高くなる事象、Bをビールの消費量が上がる事象とする。
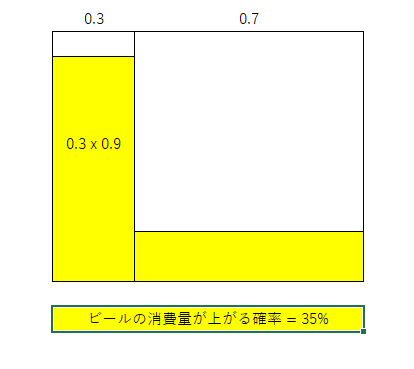
気温が高くなる確率を30%とする、またビールの消費量が上がる確率を35%とする。気温が高くなったときにビールの消費量が上がる確率を90%とする。
事前確率 : 気温が高くなる確率
尤度 : 気温が高くなったときにビールの消費量が上がる確率(90%)。P(ビールの消費量が上がる | 気温が高い) という条件付確率
事後確率 : またビールの消費量が上がった前提で、気温が高い確率。P(気温が高い | ビールの消費量が上がった)という条件付確率
これを図にまとめると以下のようになる。
条件付確率について以下が成り立つ。
P(X|Y) = P(Y|X) x P(X) / P(Y)
これはつまり
事後確率 = 尤度 x 事前確率 / P(Y)
よって
P(X|Y) = 0.9 x 0.3 / 0.35 = 0.77
すなわち、ビールの消費量が上がった時に、気温も上がっている確率は77%となる。ビールの消費量が上がっているからと言ってすぐ気温を原因にすることはできないことがわかる。