判別式の手順
- 散布図をプロットしてみてグループに分けることができるかを検討する
- 判別式のモデル(線形判別、マハラノビスなど)を検討する
- データを読み込み判別式テンプレートを作成する
- 判別式を作成する
- 判別的中率を計算し判別式が適当であるかを判断する
- データの予測に用いる
PDCAサイクルで判別式を利用してみる。Pではビジネス上の戦略および経験から適切となる判別式を作成する。Dでは判別式を利用して商品展開などを実施してみる。CではDの結果と判別式の結果を比較する。結果が一致していれば改善の余地がないかを検討する。乖離しているようならば、要因を検討する。AではDに基づいて式を改善したりオペレーションでの対応を検討する。
データの検討
今回のデータは多変量解析がわかった 日本実業出版社を参照している。
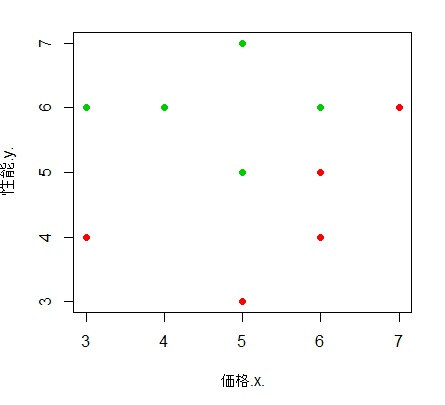
まずデータについて散布図を作成してみて、グループに分かれているかを検討する。
> sales <- read.csv("data01.csv")
> sales
価格.x. 性能.y. 購入フラグ
1 4 6 ○
2 5 7 ○
3 3 6 ○
4 5 5 ○
購入フラグで色分けをして散布図を作成する。
> plot(価格.x., 性能.y., pch=19, col=as.numeric(購入フラグ)+1)
グループに分かれていると判断できたので判別式を計算する。
線形判別式の算出
今回はエクセルのソルバーを利用して判別式を算出する。
テンプレートの作成
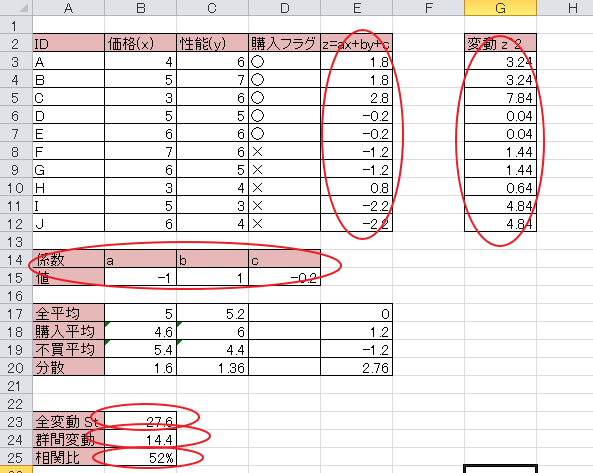
線形判別式として z=ax+by+cを考える。
初期値としてa=-1, b=1を考える。(B15,C15)
次にz=ax+by+cをすべてのレコードに対して計算する。(E3~E12)
zの平均が0になるようにcを設定する。このときz=0.2となったのでc=0-0.2とする。
全変動 Stは変動 z^2と合計となる。( SUM(G3:G12) )
群間変動は 購入の観察数x (購入平均z-全平均z) ^2 + 不買の観察数x(不買平均z-全平均z)となる。 ( 5*(E17-E18)^2 + 5 * (E17-E19)^2 )
ソルバーの実行
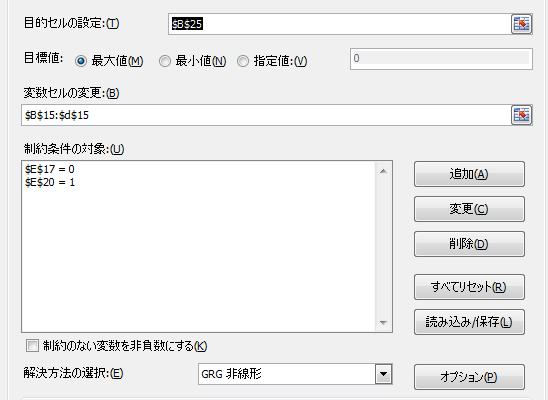
ソルバーのターゲットは相関比を最大値にする。よって目的セルの設定は$B$25であり目標値は最大値。
変更する値はa, b, cであるので、変数セルはB15~D15
Zの正負で購入・不買を判断するためにzの平均値=0を条件とする。またzの分散=1とすることでa, bが定まるようにする。分散を指定しないとa, bの比率のみとなる。
ソルバーを実行する。
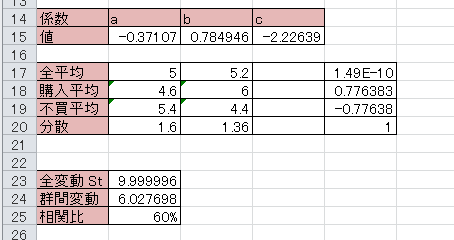
実行した結果、線形判別式は z=-0.37x + 0.78y – 2.2となり、相関比は60%となった。これは全変動のうち6割が群間変動であることを意味する。
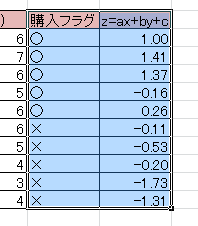
判別得点
判別得点を見てみると一件のレコードを除き正しく判別されていることがわかる。
また的中率は 9/10 = 90%となる。