主成分分析の手順
- データが分離できるか検証する
- 主成分負荷量と寄与率を求める
- 新しい変数に名前を付ける
- 変量プロット
- 主成分プロット
今回はRで提供されているirisを使う。主成分分析の前段階である検証はRで実施するが主成分分析の実行はエクセルのソルバーを用いる。
主成分分析を数学的に解く手順
- 制約条件 / 分散最大
- ラグランジェの解法
- 固有値問題への帰結
- 累乗法
- 固有値
- 固有値を主成分の分散に変換
主成分分析のメモ
- 主成分分析で求めるのは主成分負荷量。求められた主成分負荷量が採用できるかは寄与率で判断する。
- 寄与率は 主成分の分散 / トータルの分散 で求める。
- 主成分には分散が大きな変数が寄与するので、各変数の分散を求めれば主成分負荷量の大きさについてある程度目安が立つ。
- 主成分負荷量が求められたら、その大きさによって名前付けを行う。名前付けをすればその変数が求められた背景が理解できる。
データの検証
irisデータを読み込み、それぞれのデータについて相関を見てみる。
> data(iris) > head(iris) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa > str(iris)'data.frame': 150 obs. of 5 variables: $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ... > pairs(iris[1:4], main="Iris", pch=19, col=as.numeric(iris$Species)+1)
データをエクセルで取り扱るようにcsvで出力
> getwd()
[1] “C:/Users/UserA/Documents”
> write.table(iris, “iris.csv”, sep=”,”)
エクセルによる主成分分析
主成分分析表を作成
データを取り込みソルバーで分析するための準備をする。
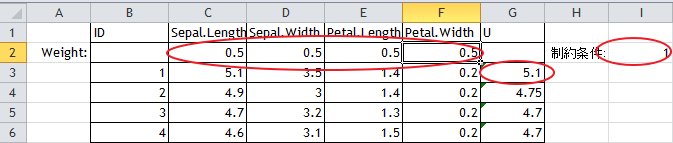
- 主成分負荷量の初期値
C2:F2は主成分負荷量を設定する。あらかじめ0.5に設定しておく。
この値はa^2+b^2+c^2+d^2=1となる制約条件に対して初期値がa=b=c=dとなるとき、4a^2=1 よって a=0.5から算出している。 - 制約条件 =C2^2+D2^2+E2^2+F2^2
- 主成分 U =SUMPRODUCT($C$2:$F$2,C3:F3)
それぞれの項目について分散を計算しておく。
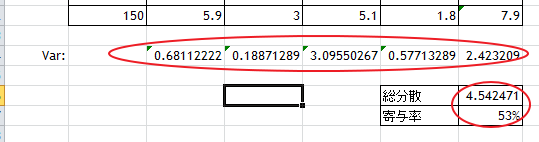
- 分散 =VARP(C3:C152)
- 総分散 =SUM(C154:F154)
- 寄与率 =G154/G156
ソルバー
ソルバーを使って主成分分析を実行する。
目的とするセルは主成分uの分散である。変化する値は主成分負荷量。制約条件として∑主成分負荷量i^2=1となるのでこれを設定してソルバーを実行する。
実行結果
実行した結果は以下のようになった。
u = 0.364 x Sepal.Length + .0859 x Petal.Length + 0.359 x Petal.Width
Sepal.Widthはuに対して全く貢献していないことがわかる。
さらに寄与度を計算してみると92%となり、主成分は全体の情報の92%と非常に高い程度で情報を説明していることがわかる。
第二主成分
第二主成分も合わせて取得する。
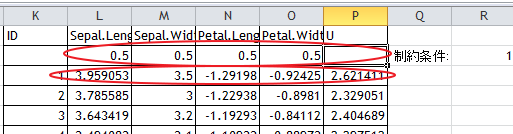
第二主成分を分析するための表を作成する。
フォーマットは第一主成分と同じであるが変数uの影響を取り除いている。
例) レコード1のSepal.Length C3-($G3*C$2)
C3はオリジナルのSepal.Length、C$2はSepal.Lengthの主因数負荷量、G3は第一主因数である。
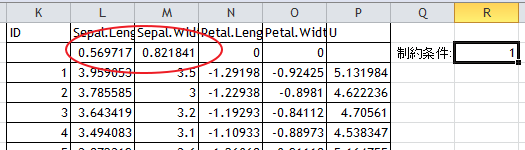
実行結果は以下のようになった。
v = 0.570 x Sepal.Length + 0.822 x Sepal.Width
寄与率は66%となった。
Rによる主成分分析
Rではprincompを使って主成分分析を実行する。
> iris.princomp <- princomp(iris[,1:4], scale=TRUE) > iris.princomp Call: princomp(x = iris[, 1:4], scale = TRUE) Standard deviations: Comp.1 Comp.2 Comp.3 Comp.4 2.0494032 0.4909714 0.2787259 0.1538707 4 variables and 150 observations. > summary(iris.princomp) Importance of components: Comp.1 Comp.2 Comp.3 Comp.4 Standard deviation 2.0494032 0.49097143 0.27872586 0.153870700 Proportion of Variance 0.9246187 0.05306648 0.01710261 0.005212184 Cumulative Proportion 0.9246187 0.97768521 0.99478782 1.000000000
固有ベクトルはloadingsに設定されている。
> iris.princomp$loadings Loadings: Comp.1 Comp.2 Comp.3 Comp.4 Sepal.Length 0.361 -0.657 -0.582 0.315 Sepal.Width -0.730 0.598 -0.320 Petal.Length 0.857 0.173 -0.480 Petal.Width 0.358 0.546 0.754 Comp.1 Comp.2 Comp.3 Comp.4 SS loadings 1.00 1.00 1.00 1.00 Proportion Var 0.25 0.25 0.25 0.25 Cumulative Var 0.25 0.50 0.75 1.00
各項目のスコアはscoresに設定されている。
> iris.princomp$scores Comp.1 Comp.2 Comp.3 Comp.4 [1,] -2.684125626 -0.319397247 -0.027914828 0.0022624371 [2,] -2.714141687 0.177001225 -0.210464272 0.0990265503 [3,] -2.888990569 0.144949426 0.017900256 0.0199683897
主成分負荷量を求める
> t(iris.princomp$sd * t(iris.princomp$loadings) ) [, drop = FALSE] Comp.1 Comp.2 Comp.3 Comp.4 Sepal.Length 0.7406268 -0.32236633 -0.16222677 0.04854424 Sepal.Width -0.1732207 -0.35848840 0.16665321 -0.04919602 Petal.Length 1.7556635 0.08512102 0.02124897 -0.07383316 Petal.Width 0.7342790 0.03705902 0.15213733 0.11596580
有効な主成分の範囲を特定する。
plot(iris.princomp, type="lines", col="blue")
これによると第二主因数までで95%以上の分散が説明されていることがわかるので第二主因数までを使えばよいことがわかる。
検証
第一主因数と第二主因数でプロットする。







[Rではprincompを使って主成分分析を実行する。]
オンラインヘルプでも,prcomp を使う方が推奨されています[ A preferred method of calculation is to use svd on x, as is done in prcomp.]
コメントありがとうございます。次回はprcompを使ってみます。