条件付き確率はベイズ統計学の基本となる。これをなるべく簡単な例で考えてみる。
あなたは夏の暑い中八百屋来ました。そこではおいしそうなスイカが売っています。過去の経験上音が「ぽんぽん」となるスイカはおよそ8割あります。甘くておいしいスイカは全体の8%あります。しかしその中で「ぽんぽん」となるスイカは10%しかありません。このとき「ぽんぽん」となるスイカを買ったときに、そのスイカがおいしい確率はどれくらいでしょうか。
まず基本となる確率は以下のようになる。
- P(おいしい) = 8%
- P(ぽんぽん) = 80%
- P(ぽんぽん∩おいしい) = 8% X 10%
さてP(ぽんぽん∩おいしい)について考えると以下の式は今回の場合成り立たない。確率の積は互いに独立でなければならないが、この条件では「ぽんぽん」と「おいしい」は
P(ぽんぽん∩おいしい) = $$P(ぽんぽん)\times P(おいしい)$$
ここで「おいしい」という前提で「ぽんぽん」となる確率を以下のように書く。
P(ぽんぽん | おいしい)
これは順番を覚えにくいがイメージとしては割り算を意識するとよい
$$(ぽんぽん | おいしい)=\frac{ぽんぽん}{おいしい}$$
この条件付き確率はP(ぽんぽん)とP(おいしい)の積で考えることはできない。なぜかを考えてみる。
先ほどの例では同じタイミング、つまりあるスイカを選んだ時にそのスイカが「ぽんぽん」でかつ「おいしい」確率を考えた。そのためにP(ぽんぽん)xP(おいしい)でその確率を計算できた。しかし今回はすでにそのスイカがおいしいとわかっている。そのためにおいしいスイカの中でどれくらいの確率でぽんぽんとなるかを考えなければならない。
P(ぽんぽん∩おいしい)を別の視点から見てみる。これは「おいしいスイカである確率」に、「おいしいスイカという条件でぽんぽんとなる確率」を掛けたものに等しくなる。「おいしいスイカという条件でぽんぽんとなる確率」は条件付き確率であり以下のように考えられる。
$$P(ぽんぽん∩おいしい) = P(おいしい)\times P(ぽんぽん|おいしい)$$
この式を変形すると条件付き確率を求める式が出る。
$$P(ぽんぽん|おいしい)=\frac{P(ぽんぽん∩おいしい) }{P(おいしい)}$$
よって以下のようになる。これは問題でもすでに10%と出ているので明らかである。
$$P(ぽんぽん|おいしい)=\frac{0.1 \times 0.08}{0.08}=10\%$$
さてP(おいしい | ぽんぽん)を考えると、次のように考えられる。
$$P(ぽんぽん∩おいしい) = P(ぽんぽん)\times P(おいしい|ぽんぽん)$$
P(ぽんぽん∩おいしい)で結びつけると、
$$P(おいしい)\times P(ぽんぽん|おいしい) = P(ぽんぽん)\times P(おいしい|ぽんぽん)$$
となる。これでぽんぽんなるときのおいしい確率であるP(おいしい|ぽんぽん)を求めることができる。
$$P(おいしい|ぽんぽん) = \frac{P(おいしい)\times P(ぽんぽん|おいしい)}{P(ぽんぽん)}$$
数を当てはめて計算する。
$$P(おいしい|ぽんぽん) = \frac{0.08\times 0.1}{0.80} = 1\% $$
つまりまとめるとぽんぽんとなるスイカでおいしいのは1%しかないのである!
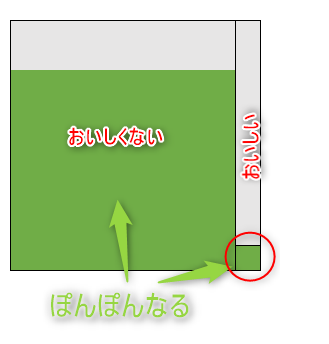
これを図にまとめる。左側の長方形が「おいしい」スイカで、その中で赤丸で囲まれた部分が「ぽんぽん」なるスイカとなる。