5章で学ぶこと
5章では検定方法について紹介している。以下の方法について検定対象と検定する条件を理解する。
- Z検定
- t検定
- 無相関検定
- 独立性の検定
また検定の手順についてもまとめている。
検定方法
| Z検定 | 平均値 | 正規分布 | 母分散σ^2が既知、一つの平均値 |
| t検定 | 平均値 | t分布 | 母分散未知、一つの平均値 |
| 無相関検定 | 相関係数 | t分布 | |
| 独立性の検定 | 質的変数の独立性、2つの質的変数の連関 | カイ二乗分布 |
検定の手順
検定対象と条件により利用する検定方法は異なるが、検定手順は同じである。以下は記載されている手順を参考にして、作った手順である。
- 検定対象を明らかにする
- 条件を明らかにする
- 検定モデルの選択
- 帰無仮説と対立仮説を立てる
- 検定統計量の選択
- 有意水準の決定
- 検定統計量の実現値を求める
- 帰無仮説の棄却、採択を決定する
この章で学ぶ検定方法の一覧
- Z検定
- t検定
- 無相関検定
- カイ二乗検定
練習問題
5-1
帰無仮説はこのサンプルデータがとられた母集団の平均は170である。対立仮説は平均は170ではない。有意水準を5%として考える。利用する統計モデルは母集団の平均値について推定する。サンプル数は20あること、および母集団は正規分布に従っているためにt検定を利用できる。
t.test()を利用してt検定を行う。
> t.test(w_length, mu=170) One Sample t-test data: w_length t = -3.8503, df = 19, p-value = 0.001079 alternative hypothesis: true mean is not equal to 170 95 percent confidence interval: 160.584 167.216 sample estimates: mean of x 163.9
上記より、自由度19のt検定を行っている。対立仮説は”not equal to 170″であり両側検定となる。
サンプルの平均=163.9であり、ここから統計量t=-3.8503が求まる。これに対応するp値は0.001079である。有意水準5%以下であることからとしたので帰無仮説は棄却できる。
母集団平均の95%での信頼区間における推定値は160.584~167.216となる。
以下t.test()の結果の参考になる情報を記載しておく。
> qt(0.025,19) [1] -2.093024 > qt(0.025,19, lower.tail=FALSE) [1] 2.093024 > pt(2.093024,19) [1] 0.975 > pt(-3.8503,19) [1] 0.000539266
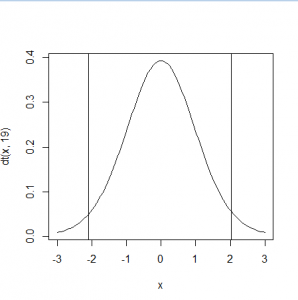
自由度19におけるt分布は以下のようなっている。
> curve(dt(x,19),-3,3) > abline(v=qt(0.025,19)) > abline(v=qt(0.972,19))

[有意水準5%以下であることから]というのは,不適切でしょう
[有意水準を5%としたので]とでも書くべき
ありがとうございます。修正しました。