ロジスティック回帰
確率を得るために
パーセプトロンの判別式により確率をとることはできない。パーセプトロンのヒンジ損失は正負のみを判断し、間違っている場合だけパラメータの更新をする。つまりぎりぎりで正解となったとしても考慮されない。またあらゆる値をとりうるために0~1となる確率は合わない。そのためにロジスティック回帰ではパーセプトロンとは異なる活性化関数と誤差関数を利用する。
シグモイド関数
実数を0~1に押し込める関数=シグモイド関数
尤度関数から交差エントロピー誤差関数
もっともふさわしいパラメータwを推定するための関数。これは各データが正解ラベルになる条件確率をすべて掛け合わす関数である。尤度関数が最も大きくなる重みwを探す。尤度関数は掛け算であり計算が面倒くさいので対数化する。さらに最小値を求める計算にするために記号を反転する。これを交差エントロピー誤差関数と呼ぶ。
正則化
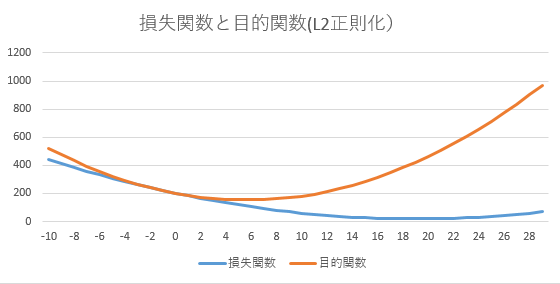
データの損失があっても、低い重みのほうが評価が高くなる(目的関数が低くなる)。
- w = -10 ~ +30
- 損失関数 = 0.5*(w-20)^2 + 20
- 正則 = w^2
正則化が弱いとすべてのパラメータがモデルに組み込まれるので過学習を起こす。この結果としてすべての訓練データを通るような曲線を生成するモデルになる。それに対して正則化が強すぎるとパラメータの重みが0に近くなってしまうために直線に近づいてくる。